"Doğada ve insan vücudunda matematiksel bir düzenin varlığı tartışmasız kabul edilmektedir. Bu düzeni açıklamak için kullanılan en eski formüllerden biri olarak altın oranı (phi:φ) görmekteyiz. Son yıllarda; M.Ö. 5. yüzyıldan beri sanat eserlerinde kullanılan, günümüzde ise karmaşık biyolojik yapılar ile işlevlerin modellenmesinde yararlanılan, fraktal özelliklere sahip irrasyonel bir sayı olan altın orana karşı yeniden bir ilgi uyanmıştır. Altın oran, Antik Yunan’dan Rönesans’a ve güncel bilimsel çalışmalara kadar insanlık tarihi boyunca zaman zaman popülerleşerek karşımıza çıkmaktadır.

Güzelliğin arkasında matematiksel bir formül olduğuna inananlar tarafından altın oran, bir 'güzellik formülü' olarak kabul edilir. Bu doğrultuda, yüz ve vücut estetiği analizlerinde her geçen gün yeni oranlar sunulmakta ve yayımlanmaktadır. Bununla birlikte, son dönemdeki bilimsel sonuçlar genellikle iki uç nokta arasında kalmaktadır: Bir yanda, birçok çalışmada φ sayısının yapay olarak ortaya çıktığını iddia eden kuşkucu araştırmacılar, güzelliğin matematiksel bir formülle ifade edilemeyeceğini savunarak bu kavramı nesnenin kendisinden ziyade biyolojik ve evrimsel temellerle açıklamaktadır. Diğer yanda ise altın oranın insan fizyolojisindeki varlığında mistik bir anlam bulan araştırmacılar yer almaktadır.

Altın Oran'ı (φ) en basit haliyle açıklamak gerekirse: Bir bütünü (bu bir nesne, uzunluk, yüzey alanı ya da hacim olabilir) eşit olmayacak şekilde ikiye böldüğümüzde; bütünü oluşturan iki miktarın toplamının büyük miktara oranı, büyük miktarın küçük miktara oranına eşitse, ortaya çıkan bu iki miktar 'altın oran' içerisindedir.

Muhtemelen matematik tarihinin en büyüleyici sayısı olan φ, yaklaşık olarak 1,618034… değerine eşit olan irrasyonel bir sayıdır. Altın Oran'ı büyüleyici kılan asıl unsur ise onun öz-benzerlik probleminin bir çözümü olmasıdır. Öz-benzerlik; bir nesnenin parçalarının bütünün geneline benzemesi, aynı yapının farklı ölçeklerde tekrarlanması özelliğidir. Bu nedenle φ, fraktal geometrinin en temel ve en basit örneği olarak kabul edilir."

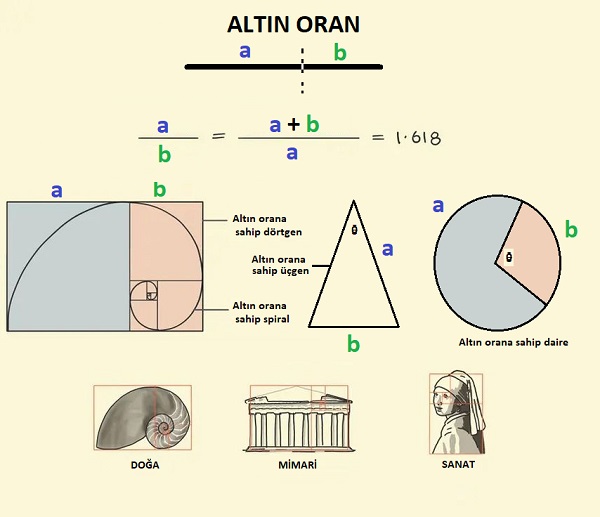
Phi muhtemelen M.Ö. 5. yüzyılda, Pisagorcuların 'ölçülemezlik matematiksel kavramını' yani irrasyonel sayıları tanımlamasıyla keşfedilmiş olmalıdır. Yunan alfabesindeki Phi (φ) harfi ile simgelenerek kaydedilmiştir. Yunanlıların bu oranı neden bir güzellik kanonu olarak seçtikleri hâlâ bilinmemektedir. Bazı araştırmacılar, bunun nedeninin altın dikdörtgenin insan görme alanına çok yakın olmasından kaynaklandığını öne sürmektedir. 1965 yılında Stone ve Collins tarafından ortaya atılan ve 'perimetrik hipotez' olarak adlandırılan bu teoride  gözlerimizin dünyayı tarama biçiminin ve iki gözün birleşik görüş alanının kabaca bir altın dikdörtgen oluşturduğunu savunur. Bu bakış açısına göre, altın oranı "güzel" bulmamızın sebebi, görsel sistemimiz için en "doğal" ve "yorucu olmayan" tarama alanını temsil etmesidir.

"Antik Yunanlıların altın oranı bir güzellik kanonu olarak seçmelerinin bir diğer olası nedeni, insan antropometrisiyle ilgili oranların da altın orana yakın olduğunun gözlemlenmesidir. İnsan figürlerini kopyalayan pek çok Yunan heykeli, altın oranlara sadık kalınarak inşa edilmiştir. Ayrıca bu durum, Antik Yunan'daki 'ideal oran' kavramı ile güzellik ve iyiliğin kusursuz birleşimi anlamına gelen kalokagathia kavramıyla da uyumludur.

Kalokagathia (kalos kai agathos), Antik Yunan'da dışsal güzellik (estetik) ile içsel erdemin (ahlak) birbirinden ayrılamaz olduğu inancını temsil eder. Platon'a göre güzellik, bakan kişinin öznel algısında değil; nesnenin kendi matematiksel ve geometrik yapısında saklıdır. Eğer bir nesne doğru oranlara (yani altın orana) sahipse, o nesne nesnel olarak güzeldir. Bu bağlamda altın oran sadece görsel bir 'güzellik' değil, aynı zamanda bir 'doğruluk' ve 'erdem' göstergesidir."

M.Ö. 300’lü yıllarda, altın oranın bilinen ilk yazılı tanımını Öklid’in Elemanlar adlı eserinin 2. kitabında görmekteyiz. Öklid, bir doğru parçasını altın orana göre bölmek için birçok önerme sunar ve bu geometrik kurgunun temelini 'aşırı ve orta oran' (extreme and mean ratio) kavramı üzerine inşa eder. Öklid kendi döneminde "altın oran" ismini kullanmıyordu (bu isim çok daha sonra verilmiştir). O, bu orana "aşırı ve orta oran" diyordu.

Bir sayı dizisinin (1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, …) izlerine, Fibonacci'den çok daha önce Hindistan’ın Sanskritçe şiir ölçülerinde rastlamaktayız. Bu dizideki her sayı, kendisinden önceki iki sayının toplamından elde edilir. Dizideki sayılar büyüdükçe, ardışık sayıların birbirine oranı altın orana (1,618...) asimptotik olarak yaklaşır(Asimptotik olarak yaklaşma bu sayı dizisindeki sayılar büyüdükçe 1.618... değere sonsuzda yaklaşmaktadır). Günümüzde 'Fibonacci dizisi' olarak bilinen bu sayı dizisi, ismini İtalyan matematikçi Leonardo Fibonacci'den almıştır. Fibonacci, 1202 yılında kaleme aldığı Liber Abaci adlı eseriyle Hint-Arap sayı sistemini Avrupa'ya tanıtmış ve bu sistemin yaygınlaşmasına en büyük katkıyı sağlamıştır.

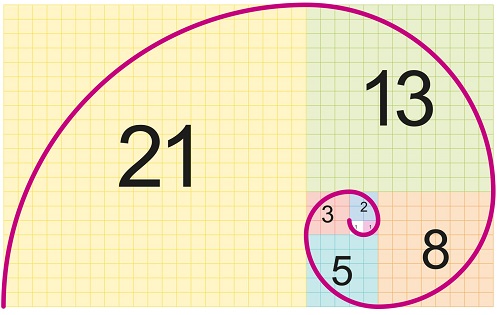
Bu tarihsel verilere karşın, 1509 yılı öncesinde altın oranın mimari bir yapıda veya resim gibi sanatsal bir eserde bilinçli olarak kullanıldığına dair somut bir kanıt bulunamamıştır. Bu durum, bir keşiş ve matematikçi olan Luca Pacioli’nin 1509’da yayımlanan ve altın oranın sanattaki önemini literatüre kazandıran ünlü eseri De Divina Proportione (İlahi Oran) kitabına kadar devam etmiştir. Pacioli, bu oranın Tanrı'nın varlığının bir kanıtı olduğunu öne sürmüştür. Pacioli'nin bu oranı "İlahi" olarak nitelemesi; onun tekliğini, bölünemezliğini ve her yerde var oluşunu mistik olarak Tanrı'nın sıfatlarıyla bağdaştırmasından kaynaklanır.

Leonardo da Vinci, Pacioli’den matematik dersleri almış ve bu eserin illüstrasyonlarını bizzat çizmiştir. Da Vinci, sadece bu kitaba çizim yapmakla kalmamış; aynı zamanda Mona Lisa ve Son Akşam Yemeği gibi başyapıtlarında kompozisyonu altın dikdörtgenler üzerine kurgulamıştır.

17. yüzyılda Kepler, φ sayısını geometrinin iki büyük hazinesinden biri olarak tanımlamış (diğeri Pisagor teoremidir) ve bu sayının Fibonacci dizisindeki ardışık sayıların birbirine oranıyla ulaşılan limit değeri olduğunu kanıtlamıştır.

Aynı yüzyılda Descartes, eş açılı (teğet ile radyal hat arasında sabit bir açıya sahip olan) logaritmik sarmalı tanımlamış; bu sarmal ilerleyen yıllarda Bernoulli tarafından spira mirabilis ('muhteşem sarmal') olarak adlandırılmıştır. Altın sarmal, öz-benzerlik özelliğine sahip olan özel bir logaritmik sarmal türüdür. Doğada deniz kabuklarından galaksilere kadar pek çok yapıda gözlemlenen bu sarmalın temel özelliği, merkezden uzaklaştıkça boyutu artsa da geometrik formunun (şeklinin) değişmemesidir. Bernoulli, bu sarmalın geometrik özelliklerinden o kadar etkilenmiştir ki mezar taşına 'Eadem mutata resurgo' (Değişmiş olsam da aynı şekilde yeniden doğarım) sözünün yazılmasını ve bir sarmal figürü kazınmasını vasiyet etmiştir. Bernoulli'nin vasiyetine rağmen, mezar taşını yapan usta bir hata yapmış ve mezar taşına logaritmik sarmal yerine Arşimet sarmalı kazımıştır.

1970'lerde Mandelbrot; farklı ölçeklerde kendini tekrar eden desenler sergileyen yapıları veya fenomenleri ifade eden fraktal kavramını matematiğe tanıtmıştır. Fraktallar, karmaşık görünen ancak basit bir kuralın sonsuz tekrarıyla oluşan yapılardır. Altın oran φ, bu bağlamda en temel fraktal sabitlerinden biri olarak kabul edilir. Mandelbrot'un fraktal geometrisi, biyolojik sistemlerin (akciğer bronşları, damar ağları, sinir sistemleri) neden pürüzsüz geometrik şekiller yerine "parçalı" ve "kendini tekrar eden" yapılar olduğunu açıklar.

El, insan anatomisinde altın oranla en sık ilişkilendirilen bölümlerden biridir. Littler (1973); parmak uçlarının hareketinin bir altın sarmal izlediğini ve falanks (parmak kemiği) uzunlukları arasındaki oranın, Fibonacci sayılarını takip ederek öz-benzer (autosimilar) bir yapı sergilediğini öne sürmüştür. Parmak uçlarının sarmal hareketi (Littler’ın ilk önermesi), elin bir nesneyi en verimli şekilde kavramasını sağladığı için kabul görmektedir. İlk önerme sonraki deneysel çalışmalarla desteklenmiş olsa da (Gupta ve ark. 1998), ikincisi çeşitli radyografik çalışmalar tarafından eleştirilmiştir. Özellikle Hamilton ve Dunsmuir (2002); falanksların fonksiyonel uzunluk oranlarının ilk dört parmak için 1:1,3:2,3; küçük parmak için ise 1:1:2 olduğunu vurgulamıştır. Falanks uzunluklarının tam olarak Fibonacci sayılarını (2, 3, 5, 8...) tutmaması, biyolojik değişkenliğin matematiksel ideallikten her zaman sapabileceğini gösterir. 

Yapı ve işlevi birleştiren benzer bir yaklaşım Tucker'ın (2000) çalışmasında görülür; Tucker, bir şahinin saldırı için en iyi uçuş yolunun sarmal olduğunu açıkça gösterir. Bunun nedeni, şahinlerin gözlerinin (yapı) başın yanlarında olmasıdır ve sadece bu yolun eş açılılığı, başı çevirip aerodinamik verimliliği kaybetmeden avla göz temasını (işlev) sürdürmeye olanak tanır.  

Choo ve meslektaşları (2012) ise tüm parmaklar için 1:0,98:2,01 şeklinde farklı oranlar saptamışlardır. Hutchinson ve Hutchinson (2010), bu verilere tamamen farklı bir yorum getirmiştir: Veriler bir 'toplam dizisi' (summative series) olarak ele alındığında, Fibonacci ilkesine uygun şekilde üçüncü terimin ilk iki terimin toplamına eşit olduğu görülmektedir. Ayrıca yazarlar, φ sayısının sadece Fibonacci dizisinin değil, aynı toplama ilkesine dayanan (ancak başlangıç sayıları farklı olan 2, 1, 3, 4, 7, 11… gibi) tüm Lucas dizilerinin de asimptotu olduğunu vurgulamışlardır.

φ sayısının matematiksel oranlarda ve geometrik şekillerde kolayca ortaya çıkması ve diğer irrasyonel sayılara (örneğin kök 3 gibi) yakınlığı, her iki yorumu da mümkün kılmaktadır. Yine de bu çalışmaların, elin sadece antropometrisini (yapısını) altın oranla ilişkilendirmekle kalmayıp, bu oranları elin işleyişiyle (fonksiyonuyla) de bağdaştırmaları dikkat çekicidir.

Benzer şekilde Wang ve ark. (2017), kolların üç fonksiyonel bölümü (el, ön kol ve kol) ile altın oran arasında anlamlı bir ilişki bulmuşlardır. Bu bulgu, yapısal ölçümlerin fonksiyonel bir anlam taşımasına dair önemli bir örnektir. El, ön kol ve üst kol arasındaki uzunluk oranlarının altın orana yakın olması; kolun bir kaldıraç olarak hareket kapasitesini ve enerji verimliliğini optimize eden bir 'biyomekanik tasarım' olarak yorumlanmaktadır."

2007 yılında fonksiyonel MR (fMRI) kullanılarak gerçekleştirilen bir çalışmada, nesnel güzelliğin kanonik bir parametresi olarak kabul edilen altın oranın varlığı araştırılmıştır. Araştırmacılar, bu oranlı yapıların beyinde bir grup kortikal nöronun (lateral oksipital girus, prekuneus ve prefrontal alanlar) yanı sıra duygusal işleme ve öz farkındalıkla ilişkili derin bir bölge olan sağ insulanın aktivasyonunu tetiklediğini keşfetmişlerdir. Bu alanların, nesnel güzelliğin nöral temelini oluşturduğu düşünülmektedir. Kortikal Bölgeler: Altın oranlı bir yapıyı gördüğümüzde beynimiz bunu "doğru" ve "geometrik olarak tutarlı" bir veri olarak işler (Lateral oksipital girus). İnsula Faktörü: İnsulanın devreye girmesi, altın oranın sadece soğuk bir matematiksel veri olmadığını, bizde derin bir "haz" veya "uyum" hissi uyandırdığını kanıtlar. Amigdala ve Öznellik: "Güzellik bakan kişinin gözündedir" sözünün biyolojik karşılığı amigdaladır. Altın orana sahip olmayan bir şeyi de kişisel anılarımız veya tercihlerimiz nedeniyle güzel bulabiliriz; ancak altın oran evrensel bir nöral tepkiyi tetikler. Nesnel güzellik, nesneye özgü matematiksel ve evrensel estetiği tanımlar. Öte yandan, öznel güzellik (kişisel beğeni) ile ilgili olan ve nesnel güzellikle çelişmeyen bir diğer sürecin ise amigdala aktivasyonu ile ilişkili olduğu gözlemlenmiştir.

İnsan kulağının dış formu, altın sarmal yapısına oldukça yakındır (Persaud-Sharma ve O’Leary, 2015); bu durum iç kulaktaki koklea (kulak salyangozu) için de geçerlidir (Marinkovic ve ark., 2012). Ancak Marinkovic ve ark. tarafından yürütülen bu çalışma, sadece iki kokleanın incelenmesiyle elde edilen gözlemleri rapor etmiştir; bu örneklem büyüklüğü, herhangi bir istatistiksel analiz için açıkça yetersizdir.

Manoussaki ve ark. (2007), sarmal yapıdaki kokleanın yalnızca kafatasında yer tasarrufu sağlayan bir 'paketleme çözümü' olduğu yönündeki geleneksel teorinin ötesine geçmişlerdir. Yazarlar, sarmalın kademeli eğriliğinin, kokleanın düşük frekanslara verdiği mekanik yanıtı güçlendirdiğini ve böylece işitme verimliliğini artırdığını göstermişlerdir. Altın sarmalın merkezine yaklaştıkça artan kıvrımı, ses dalgalarının hidrodinamik olarak daha etkili iletilmesini sağlamaktadır. Bunun yanı sıra, kulak kepçesinin (auricula) eş açılı sarmal formu, ses dalgalarının toplanmasını ve iç kulağa doğru odaklanarak yakınsamasını kolaylaştıran bir akustik avantaj sunmaktadır.

Mitchison (1977), bitkilerdeki filotaksinin (yaprak dizilişi) Fibonacci dizisini takip ettiğini ortaya koyarken; 2011 yılında Ashrafian ve Atasiou, kalpteki damar dallanma sayısının da aynı diziyi izlediğini göstermişlerdir. Hatta 2003 yılında Gibson ve ark., kalpteki koroner arterlerde görülen aterosklerotik lezyonların bile Fibonacci sayılarına uygun şekilde dağıldığını belirtmişlerdir. Çok sayıda denekten elde edilen verilere dayanan bu çalışma; koroner arter lezyonlarının medyan konumunun, arter başlangıcı ile uç noktası arasındaki uzunluğun %23,6’sında (0,236 değeri) olduğunu göstermiştir. Bu değer phi sayısının kuvvetleriyle ilişkili bir oran olduğundan yazarlar, çalışmalarının 'insan kalbindeki koroner arter lezyonlarının dağılımında Fibonacci kaskadı ve altın oranın varlığını kanıtlayan ilk çalışma' olduğu sonucuna varmışlardır. Bu yapısal bulgunun temelinde tıpkı bitki yapraklarında ve tohumlarında olduğu gibi, kalp kası miyokardın kanla beslenmesini maksimize etmek için koroner damarların dağılım modellerini optimize etmektedir. Altın oran, sınırlı bir alandaki 'paketleme' yapılarının verimliliğini optimize eder. Fraktal benzeri bu dallanmanın, kan akışını en az enerji harcayarak en geniş alana yaymak (verimlilik) için altın oranı kullandığı savunulmaktadır. Yine de bu geometrik düzenin arter lezyonlarının konumunu tam olarak nasıl etkilediği belirsizliğini korumaktadır ve verilerde yüksek oranda bireysel değişkenlikler mevcuttur.

2013 ve 2015 yıllarında ülkemizde kardiyoloji uzmanları tarafından yürütülen çalışmalarda; kalbin kasılma (sistol) ve gevşeme (diyastol) evrelerinin süreleri, sol ventrikülün diyastol ve sistol sonu çapları arasındaki oran ile EKG üzerindeki iki ardışık kalp atımı (R-R aralığı) süresinin diyastol süresine oranının phi sayısına çok yakın olduğu saptanmıştır. Ancak bu verilere yönelik ciddi metodolojik eleştiriler yöneltilmiştir. Bu eleştirilerin odağında, çalışmadaki oranların her bir denek için ayrı ayrı hesaplanması yerine; diyastolik/sistolik süreler veya R-R aralıklarının genel ortalama değerleri üzerinden hesaplanmış olması yer almaktadır. Bu çalışmaların bilimsel çevrelerde asıl tepki çeken yönü ise sonuç bölümlerindeki ifadelerdir. Yazarların sonuç kısmında, 'kalbimiz 1,618 oranında atarak Tanrı tarafından kurulan evrenin güzel düzenine itaat etmektedir' veya 'ruhlarımız kalplerimizde ikamet eder' gibi ifadelere yer verdikleri görülmektedir. Kardiyolojide altın oranın varlığına mistik ve dini bir anlam yükleyen bu yaklaşımlar, bilimsel tarafsızlık ilkesi gereği sert bir şekilde eleştirilmiştir. Altın oranın matematiksel bir fenomen olarak incelenmesi ile ona metafizik anlamlar yüklenmesi arasındaki çizginin korunması, bilimsel güvenilirlik açısından hayati önem taşımaktadır.

2013 yılında Iosa ve meslektaşları, insan yürüyüşündeki evreler arasındaki oranın altın oranla (phi) örtüştüğünü saptamışlardır. Yürüyüş sırasında bir ayağın yere temas etmesinden aynı ayağın tekrar yere temas etmesine kadar geçen süreç 'yürüme döngüsü' (Gait Cycle) olarak tanımlanır. Bu döngü; duruş (stance) ve salınım (swing) evrelerinden oluşur. Duruş evresi, ayağın yerle temas ettiği süreci kapsarken; salınım evresi ayağın havada ilerlediği kısımdır. Duruş evresi topuk vuruşuyla (foot strike) başlar ve parmak kalkışıyla (foot off) sona erer; salınım evresi ise bu noktada başlayıp bir sonraki topuk vuruşuyla tamamlanır. Sağlıklı bir yürüyüşte ayak, döngünün yaklaşık %62’sinde yerde (duruş), %38’inde ise havadadır (salınım). Bu sürelerin birbirine oranı (62/38), yaklaşık olarak 1,63 değerini verir ki bu, altın oran olan 1,618 ile çarpıcı bir benzerlik göstermektedir. Yürüme hızı kişiden kişiye farklılık gösterse de bu çalışmaya göre adım içindeki 'altın oranlı zamanlama' neredeyse hiç değişmemekte, sabit bir biyomekanik imza olarak kalmaktadır. Ayağın yerden kesildiği an, döngünün tam 'altın kesim' noktasına denk gelmektedir. Bu bulgu; altın oranın sadece statik bir estetik parametre değil, aynı zamanda hareket verimliliği ve dinamik denge için temel bir biyolojik ritim olduğunu savunmaktadır.

 

Yukarıda açıklanmaya çalışıldığı üzere altın oran (φ); sadece ilahi ve mistik bir kavram olmanın ötesinde, doğanın seçtiği enerji verimliliği ve alan optimizasyonu stratejilerinin biyolojik bir zorunluluğu olarak tartışılmaktadır. Doğada birbirinden tamamen farklı görünen çok çeşitli biyolojik sistemler; doğrudan φ sayısı, altın sarmal veya Fibonacci dizisi ile ilişkili benzer armonik özellikler sergilemektedir. Bu bağlantı, temel olarak öz-benzerlik (self-similarity) —yani matematikteki fraktal geometrinin temeli— ile ilişkilidir. Öz-benzerlik; bir yapının farklı ölçeklerde aynı geometrik özellikleri paylaşması ve kendisinin birden fazla küçük kopyasından oluşan bütünsel bir imaja sahip olmasıdır. Bunun en ikonik örneği Romanesko brokolisidir. Matematiksel mükemmelliğiyle bilinen bu sebze, her bir küçük tomurcuğunun tüm brokolinin minyatür bir kopyası olması nedeniyle öz-benzerlik kavramını açıklamak için kullanılan en yaygın örnektir. Bu 'öz-benzer' yapıları insan fizyolojisinde; akciğer hava yollarının dallanmasında, vasküler (damar) sistemde ve karmaşık sinir ağlarında da görmekteyiz. Doğada phi'ninde bir parçası olduğu fraktal geometriye ait olan bu öz-benzerlik gözlemi bu durumun sadece bir kurala bağlı olmayan bir olasılık dağılımıyla(rastlantısal) gerçekleşmiş olduğu, yoksa bu matematiksel yapının enerji tasarrufu, maksimum yüzey alanı veya minimum direnç gibi biyolojik bir avantaj sağlayıp sağlamadığı sorusunu getirmektedir. Doğadaki bu geometrik düzenin bir "tasarım hatası" değil, fiziksel kısıtlamalar altında gelişen en verimli organizasyon biçimi olduğunu düşünülmektedir.

Altın oran bir "süs" değil, sınırlı bir hacme (göğüs kafesi, kafatası vb.) devasa bir yüzey alanını (akciğer alveolleri, beyin kıvrımları vb.) sığdırmanın en verimli yoludur.

Altın Oran, Phi ve Estetik Olarak Güzel Algısı  

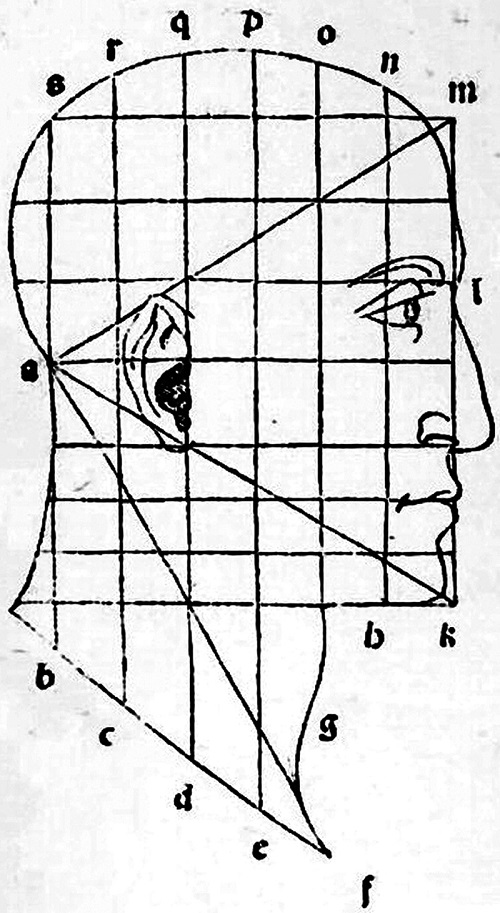
Antik Yunanlıların phi oranından büyülenerek bu oranı bir güzellik standardı olarak kullandıklarını, günümüze kadar ulaşan mimari ve sanatsal eserlerinde görmekteyiz. Hatta phi sayısının düşünsel parıltısından etkilenerek bu oranı 'altın oran' olarak tanımlamışlardır. Ancak Antik Yunanlılar ne Fibonacci dizisini ne de logaritmik sarmalı biliyorlardı; bu nedenle altın oran ile bu matematiksel kavramlar arasındaki derin bağlantıdan habersizdiler. Buna karşın, altın oranın doğada ve özellikle insan antropometrisinde (vücut ölçülerinde) var olduğuna kesinlikle inanıyorlardı. Bu inancın en ünlü yansıması Leonardo da Vinci'nin Vitruvius Adamı çalışmasında görülmektedir; benzer antropometrik araştırmalar günümüze kadar devam etmiştir.

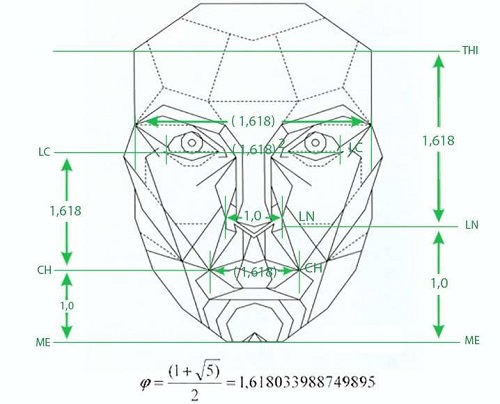
Bu tür çalışmalardan bazıları, ortalama bir insan vücudunda göbek deliği ile ayak arasındaki mesafenin tüm boy uzunluğuna oranının $\phi$ olduğunu bildirmektedir. Benzer şekilde başın tepesi ile parmak uçları arasındaki mesafe ile boy uzunluğu arasında da bu oranın mevcut olduğu iddia edilmektedir. Dahası, yüzün bir 'altın dikdörtgen' oluşturduğu; ağız, burun ve gözlerin, yüz yüksekliğinin altın kesim noktalarına yerleştiği savunulmaktadır.

Altın oranın estetik özellikleri üzerine yapılan ilk deneysel araştırmalar, modern psikolojinin kökenlerine kadar uzanmaktadır. Deneysel psikolojinin ve 'estetik psikofiziği' alanının kurucusu kabul edilen Alman fizikçi ve filozof Gustav Fechner, 1860'lı yıllarda yaptığı çalışmalarda; taban ve yükseklik oranları farklı on dikdörtgen arasından en çok tercih edilenin oranının her zaman altın orana (phi ≈ 1,618) yakın olduğunu saptamıştır. Fechner, bu deneyden hareketle altın orana sahip geometrilerin insan algısı için daha estetik olduğu sonucuna varmıştır. Ancak benzer bir deneyde dikdörtgenler yerine elipsler kullanıldığında; en çok tercih edilen formun (%42 ile) iki ekseni arasında 1,5 oranına sahip elips olduğu, altın oranlı elipsin ise %16 ile ikinci sırada kaldığı görülmüştür. Çalışmaya üçgenler de dahil edildiğinde; dikdörtgenler için phi sayısına yakın oranlar tercih edilse de elips ve üçgenlerde bu durumun geçerli olmadığı saptanmıştır. Fechner'ın dikdörtgenlerdeki başarısının elipslerde tekrarlanmaması, altın oranın "evrensel bir estetik anahtar" olduğu iddiasına karşı sunulabilecek en güçlü ampirik (deneyci) kanıtlardan biridir. Sonraki yıllarda yapılan benzer çalışmalar; phi oranının estetik üzerinde tek başına net bir etkisinin olmadığını, seçimlerimizde 1, 1,5, kök 2 veya kök 3 gibi diğer matematiksel oranların 'karıştırıcı faktör' (confounding factor) olabileceğini düşündürmüştür. Bu matematiksel oranlara verilen estetik tepkilerin; bireyin yaşına, kültürüne ve duygusal olarak içe veya dışa dönük (introvert/extrovert) kişilik yapısına göre değişkenlik gösterebileceği öngörülmektedir.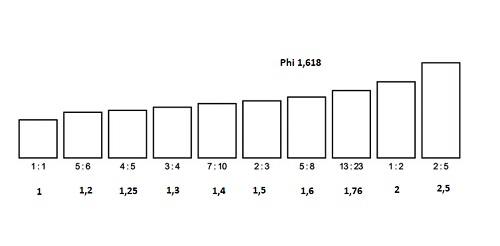

Örneğin 2017 yılında Güney Korede yapılan bir çalışmada 100'den fazla geleneksel Kore objesi kullanılarak oran tercihlerine yönelik yapılan deneysel bir çalışmada katılımcılar altın oran yerine belirgin bir şekilde karekök 2 oranını (1:1,414) tercih ettiklerini ortaya koymuştur. Bu oran matematikte kök 2 oranı olarak bilinir. Bu oran, uluslararası standart kağıt boyutlarının (A4, A3 vb.) temelidir. Özellikle Uzak Doğu mimarisi ile sanatında sıklıkla karşımıza çıkar. Bu çalışmaya dayanarak, altın oranın tercih edilen bir oran olabilmesine rağmen, iyi bir tasarım için her zaman en iyi oran olmadığı düşünülmektedir.  

Seghers, Longacre ve de Stefano (1964), insan yüzü oranlarını modellemek için altın oran kullanımını öneren ilk isimlerdir. Yüz estetiğinde altın oranın varlığı ise 1982 yılında Ricketts tarafından gösterilmiştir. Ricketts’in bu çalışmasında, dergi reklamlarından seçilen yalnızca 10 fotoğraf (7 Beyaz, 2 Asyalı ve 1 Siyah birey) analiz edilmiştir. Ricketts, 'güzel' kadın yüzlerinin armonik olduğunu ve bu armoninin, yüzün belirli yatay ve dikey oranlarında phi sayısının bulunmasına dayandığını iddia etmiştir. Bu oranlar arasında ağız genişliği/burun genişliği, göz dış kenarları arası mesafe/ağız genişliği ve yüz yüksekliğinin belirli segmentleri (örneğin; göz bebeklerinden çeneye kadar olan mesafe ile saç çizgisinden göz bebeklerine kadar olan mesafe oranı) yer almaktadır.

Ricketts'in bu hipotezi üzerine sonraki yıllarda yapılan çalışmalar çelişkili sonuçlar ortaya koymuştur. Örneğin Rupesh ve ark. (2014), altın oranın yalnızca estetik olarak 'güzel' kabul edilen yüzlerde bulunduğunu saptamış; bu oranın cerrahi veya ortodontik müdahalelerde mutlak bir kural değil, yardımcı bir 'rehber' olarak kullanılabileceğini belirtmiştir. Öte yandan Kiekens ve ark. (2006) tarafından elde edilen bulgular istatistiksel açıdan oldukça çarpıcıdır. Yazarlar, güzellik algısının %84'ünün altın oran dışındaki faktörlere (asimetri, cilt dokusu, kültürel tercihler vb.) bağlı olduğunu; dolayısıyla altın oranın tek başına belirleyici bir klinik kıstas olamayacağını savunmuşlardır. Kiekens, çalışmasında ölçülen 19 farklı orandan sadece 4'ünün, estetik puanı düşük olan yüzlere kıyasla altın orandan daha az sapma gösterdiğini saptamıştır.

1990’larda estetik cerrah Stephen Marquardt, güzelliğin altın oran ile doğrudan ilişkili olduğunu savunmuş; bu ilişkinin cinsiyet, ırk ve kültürden bağımsız olarak evrensel bir geçerliliğe sahip olduğunu ileri sürmüştür. Dr. Marquardt, bu hipotezini somutlaştırmak amacıyla 'ideal' yüz oranlarını belirlediği iddia edilen geometrik bir şablon olan **'Marquardt Maskesi'**ni geliştirmiştir. Bu maske, ongenler ve beşgenlerin karmaşık bir kombinasyonundan oluşmaktadır; bu geometrik şekillerin köşegenlerinin kenarlara oranı matematiksel olarak doğrudan altın oranı vermektedir. Marquardt Maskesi'nin, insan yüzünün ulaşabileceği en estetik formu sunduğu iddia edilmiştir. Günümüzde bu maske, yüz çekiciliğini ölçmek için objektif bir sistem olarak kabul görmekte ve yüz estetiğinde matematiksel bir model olarak referans alınmaktadır. Literatürdeki çalışmalar, genel algıda 'çekici' ve 'güzel' olarak nitelendirilen kadın yüzlerinin, bu maske modeliyle yüksek düzeyde korelasyon gösterdiğini saptamıştır. Bu nedenle birçok plastik cerrah, hastaların ameliyat öncesi planlamalarında ve ameliyat sonrası sonuçların değerlendirilmesinde bu maskeyi bir analiz aracı olarak kullanmaya devam etmektedir.

1995 yılına gelindiğinde Green tarafından hazırlanan bir derlemede Phi nin esteteik özelliklerini başarılı bir şekilde özetlenmiştir. Green bu derlemede; altın oranın estetik üzerine bulgularını savunanlar ile bu oranı, prosedür hatalarıyla taraflı hale gelmiş psikolojik çalışmalardan türetilen 'antik bir matematiksel hurafe' olarak gören şüpheciler arasında bir ikilem sunar. Green her iki yaklaşımı da kaba ve yüzeysel bulur. Şu sonuca varır: Altın oranın estetik etkisi aynı anda hem gerçek hem de kırılgandır."

Altın oran, insan yüzü oranlarını modellemek amacıyla pek çok araştırmacı tarafından önerilmiş (Goynumer ve ark., 2011; Anand ve ark., 2015; Alam ve ark., 2015) ve bu doğrultuda yüz cerrahları tarafından klinik uygulamalara dahil edilmiştir. Altın oran teorik bir düzlemden çıkarılıp estetik cerrahisinde nsomut bir uygulama kılavuzuna dönüştürülmüştür. Altın oranın kullanımı yalnızca yüz estetiği değerlendirmeleriyle sınırlı kalmayıp vücut estetiği operasyonlarına da yansımıştır. Örneğin, abdominoplasti (karın germe operasyonu) sonrasında göbek deliğinin ideal estetik pozisyonda yeniden konumlandırılması, vücut segmentleri arasındaki altın oran parametrelerine göre planlanmaktadır. Benzer şekilde, meme estetiği operasyonlarında areola kompleksi ve meme hacmi dengelenirken altın oran bir rehber olarak kullanılmaktadır. Minimal invaziv işlemlerde de bu oranın izlerini görmek mümkündür; yanak bölgesine yapılan hyaluronik asit dolgu uygulamalarında, 'malar projeksiyon' için en doğru enjeksiyon noktasının belirlenmesinde phi oranından yararlanılmaktadır. Altın oran artık sadece müzelerdeki heykellerde değil, ameliyathanelerdeki neşter izlerinde ve dolgu enjektör noktalarında da yaşıyor.

2019 yılında yayımlanan kapsamlı bir çalışma, 2001 ile 2015 yılları arasındaki güzellik yarışması birincilerinin fotoğraflarını; neoklasik kanonlar (klasik güzellik ölçüleri) ve yüzdeki altın oran parametreleri üzerinden karşılaştırmalı olarak incelemiştir. Neoklasik kanonlar, Antik Yunan heykeltıraşlığındaki yerleşik ölçü kurallarından türetilmiş; daha sonra Leonardo da Vinci, Vitruvius, Bergmüller ve Dürer gibi Rönesans sanatçıları tarafından insan yüzüne uyarlanmıştır. Bu kanonlar, yüzü yatayda üç eşit parçaya (üçte birler kuralı) veya dikeyde beş eşit parçaya (beşte birler kuralı) bölen standartlar bütünüdür. Her ne kadar bu kanonlar günümüzde tıbbi çizerler, anatomistler ve estetik cerrahlar tarafından 'ideal yüz' analizinde kullanılmaya devam etse de; belirli bir dönemdeki azınlık bir gruptan türetilen bu standartların toplumun genelini temsil etmediği vurgulanmaktadır. Neoklasik kanonlar; Çin, Arap, Türk, Hırvat, Kore-Amerikan, Afro-Amerikan ve Yunan gibi farklı etnik kökenlerin yüz yapılarındaki karakteristik çeşitlilik nedeniyle evrensel geçerliliğini yitirmiştir. Literatürde bu kuralların, 'Kafkas' (Caucasoid) ırkı örneklemlerinde, 'Mongoloid/Asyalı' ırklara kıyasla daha uyumlu olduğu saptanmıştır. Güzellik standartlarının sadece zamana göre değil, etnik köken ve coğrafyaya göre de dramatik şekilde değişmesi; Avrupa merkezli 'altın oran' veya 'neoklasik kanonların' evrensel birer formül olarak dayatılmasını bilimsel olarak tartışmalı hale getirmektedir. Evrensel güzellik iddiasını, antropolojik ve sosyokültürel bir süzgeçten geçirerek bir denge kurulmalıdır. Özellikle "Kafkas ırkı merkezli" güzellik algısının diğer etnik kökenlerle olan uyumsuzluğu unutulmamalıdır. 

Asyalı kadın denekler üzerinde yapılan bir çalışma; en çekici bulunan grubun yüz profilinin (alından çeneye kadar olan yumuşak doku hattının) en az konveks (dışbükey) yapıya, daha geniş bir alna ve daha geniş yüz hatlarına sahip olduğunu ortaya koymuştur. Bu bulgular, Avrupa merkezli dar ve daha projeksiyonlu (belirgin) yüz idealleriyle tezat oluşturmaktadır. 

Güney Kore'de 2012 Miss Korea yarışmacıları üzerinde yürütülen ve bu grubun genel popülasyonla karşılaştırıldığı çalışmada da benzer özgün veriler elde edilmiştir. Miss Korea grubunun, genel popülasyona kıyasla şu özelliklere sahip olduğu saptanmıştır:

• Daha fazla toplam yüz yüksekliği ve artmış göz genişliği,

• Daha az alt yüz yüksekliği (daha kısa alt çene bölgesi),

• Daha geride konumlanmış (retrüde) ve küçük alt dudaklar,

• Genel popülasyona göre daha küçük ve zarif bir çene yapısı.

Asya kökenli yüz morfolojisindeki bu farklılıklar, güzellik standartlarının biyolojik bir "sabit"ten ziyade coğrafi bir "değişken" olduğunu kanıtlar niteliktedir.

2009 ve 2010 yıllarında İtalyan güzellik yarışması birincileri üzerinde yapılan çalışmalar, bu bireyleri genel popülasyonla karşılaştırmıştır. Çekici bulunan kadınların; daha belirgin yüz profillerine, artmış üst yüz genişliğine ve orta yüz derinliğine (elmacık kemikleri ve burun bölgesi), daha geniş bir ağız yapısına ve daha hacimli dudaklara sahip olduğu saptanmıştır.

Yehezkel ve Turley, 1940'lardan 1990'lara kadar moda dergilerinde yer alan Afrikalı Amerikalı kadın modelleri inceleyerek, güzellik algısının zamansal değişimini ortaya koymuşlardır. Dudak pozisyonu, nazolabial açı (burun-üst dudak açısı) ve interlabial açı (dudaklar arası açı) açısından on yıllar içinde anlamlı farklar gözlemlenmiştir. Özellikle son yıllarda, çekici bulunan Afro-Amerikan kadınlarda dudak dolgunluğunun arttığı ve dudakların daha anterior (önde) konumlandığı saptanmıştır. Bu durum, estetik standartların dinamik yapısını kanıtlamaktadır.

Mommaerts ve Moerenhout’un güncel veriler (People ve FHM dergileri) üzerinden yürüttüğü çalışma, en beğenilen 15 kadın yüzünü klasik heykel oranlarıyla kıyaslamıştır. Sonuçlar, güncel 'güzel' yüzlerin klasik yüz endeksinden (facial index) anlamlı derecede sapma gösterdiğini; modern yüzlerin klasik oranlara kıyasla daha geniş bir yapıya veya daha kısa bir yüz yüksekliğine sahip olduğunu ortaya koymuştur.

Iglesias-Linares ve ark. (2011), 'En Güzel 100 Kişi' listesindeki Siyah ve Beyaz bireyleri karşılaştırdıklarında; alt yüz üçte birlik açısı, labiomental açı (alt dudak-çene açısı), yüz konveksite açısı ve alt dudak projeksiyonu açısından şaşırtıcı benzerlikler saptamışlardır. Yazarlar; küreselleşme ve çok etnikli toplulukların yaygınlaşmasıyla modern toplumun klasik 'yüz güzelliği' kavramını dönüştürdüğü sonucuna varmışlardır. Etnik kökenden bağımsız olarak, günümüzün 'güzel' kadınları, Siyah ve Beyaz morfolojik özelliklerinin harmonize olduğu bir 'melez' güzellik algısını temsil etmektedir. Bu yeni standart, neoklasik kanonların ve altın oranın modern dünyada neden tek başına yeterli bir kıstas olamadığını açıklamaktadır. 

Modern güzellik algısını yansıtan yüz oranları, tarihsel standartlardan belirgin şekilde farklılık göstermektedir. Güncel fotogrametrik analizler; geçmişin neoklasik ideallerine kıyasla daha uzun bir alın yapısı, daha ince bir alt-üst dudak yükseklik oranı, daha geniş bir interala-medial canthus (burun kanadı-iç göz pınarı) oranı ve daha geniş bir nazofrontal açı sergilemektedir. Kâinat Güzeli (Miss Universe) birincileri üzerinde yapılan incelemeler, bu bireylerin geleneksel kanonlara göre daha geniş bir nazofasiyal açıya ve daha belirgin bir burun ucu projeksiyonuna sahip olduklarını göstermiştir. Dahası, yapılan istatistiksel analizler yüzdeki altın oran parametrelerinin, modern güzellik algısını tanımlamada anlamlı derecede yetersiz kaldığını saptamıştır. Retrospektif nitelikteki bu veriler, güncel estetik cerrahi planlamalarında 'evrensel formüller' yerine 'dinamik standartların' kullanılması gerektiğini ortaya koymaktadır. Güzellik algısı küreselleşme, etnik çeşitlilik ve zamansal değişimlerle şekillenen dinamik bir süreçtir. Güzellik artık tek bir formülün dar sınırlarına sığmamakta; farklı kültürlerin, biyolojik gerçekliklerin ve modern estetik eğilimlerin harmonisinde yeniden tanımlanmaktadır.

Tüm bu çalışmalar altın orana yönelik estetik bir tercihin varlığını sorgulasa da, bu tercihin arkasında yatan temel motivasyonları tam olarak açıklayamamaktadır. Bu noktada Oyun Teorisi (Game Theory; Schuster, 2017; Suleiman, 2017), estetik tercihlere yönelik özgün bir yaklaşım sunmaktadır. Stratejik karar alma süreçlerini matematiksel olarak inceleyen Oyun Teorisi, belirli bir kaynağın (örneğin bir miktar paranın) iki kişi arasındaki paylaşımında 'adil' ve 'istikrarlı' bir dengenin kurulmasını belirli bir oranla ilişkilendirir. Yapılan araştırmalar, kaynağa sahip olan kişinin paylaşım sırasında 50/50 şeklindeki tam simetrik bir bölünme yerine, asimetrik fakat dengeli bir oranı tercih ettiğini göstermektedir. Bu kurama göre en 'adil ve istikrarlı' paylaşım; kaynağın tamamının kişiye kalan kısmına oranının, karşı tarafa verilen kısmın teklif sahibine oranına eşit olduğu noktada, yani altın oranda (phi) gerçekleşmektedir. Dolayısıyla birey, sahip olduğu içsel uyum mekanizması nedeniyle statik bir eşitlik (50/50) yerine, dinamik ve asimetrik bir paylaşım olan altın oranı seçmektedir. Belki de phi, eşitsizliğin matematiksel olarak en dengeli, kabul edilebilir ve sürdürülebilir olduğu 'altın nokta'yı temsil etmektedir. Altın oran sadece biyolojik veya estetik bir olgu değil, aynı zamanda davranışsal ve sosyal bir denge noktasıdır. Oyun Teorisi buradaki asimetrinin neden "kaos" değil de "uyum" olarak algılandığına dair matematiksel bir zemin hazırlıyor.

Altın oran, bir teori olarak büyüleyici derecede basit ve etkileyicidir; ancak nihayetinde eksiktir. Güzelliği nicel terimlerle tanımlamaktan hâlâ çok uzağız; öyle ki güzellik, modern bilimsel verilere rağmen gerçekten de 'bakan kişinin gözündedir'. Evrensel bir estetik kriteri olarak kullanımı defalarca çürütülmüş olsa da altın oran hâlâ 'güzeldir'; çünkü yaşamın ve doğanın temel formunu yansıtmaktadır. 

Altın oran, zamanı aşan mutlak bir güzelliği tanımlamaya duyulan özlemin yarattığı entelektüel bir hayaldir. Diğer bir deyişle, insan vücudunun oranlarında aranan bu sayısal uyum, sayılara duyulan mistisizmden türetilmiş felsefi bir kurgudur; yani insanoğlunun matematiksel kesinliğe duyduğu estetik arzuyu yansıtır.

Altın oran, katı bir bilimsel gerçeklikten ziyade, insanların doğada bir düzen ve hakikat arayışının tezahürüdür. Doğada ve insan vücudunda matematiksel bir düzenlilik bulunabilir; ancak bu durum, matematikte evrensel ve değişmez bir 'güzellik formülü'nün mevcut olduğu anlamına gelmemektedir. Modern estetikte artık biliyoruz ki; 'güzelliğin özü', nesnenin kendisindeki matematiksel bir 'güzellik formülünden' türetilemez.  Bunun yerine güzelliğin, matematikten ziyade biyolojik ve evrimsel süreçlerle şekillendiği vurgulanıyor.

Sonuç

Antik Yunan'ın estetik algısından başlayıp, modern nörobilim ve biyomekaniğe kadar uzanan Phi'nin bu yolculuğuna bakıldığında şu sonuçları çıkarmak zorundayız. 

Birinci nokta, phi sayısının matematiğin birçok alanlarıyla çok sayıdaki bağlantısı bulunmakta. Phi sayısı Fibonacci dizisiyle,  beşgen geometrisiyle, sarmallarla, öz benzerlikler( Bir yapının bütününün, parçalarıyla aynı geometrik orana sahip olmasıdır) ve fraktallar ile ilişkilidir. Bunlar altın oranın 'müttefikleri' olarak tanımlanabilir. Ancak, Fibonacci sayıları ile insan parmak uzunlukları, kalp veya kalp damar dallanma sayıları arasında benzerlikler bulmak, altın oranla mutlaka katı bir ilişki olduğu anlamına gelmez. Fibonacci dizisinde (1, 1, 2, 3, 5, 8...) ardışık sayıların birbirine oranı başlangıçta tam olarak 1,618 değildir. Sayılar büyüdükçe, limite gittikçe bu oran phi değerine sonsuzda yaklaşır. İnsan vücudundaki küçük sayıların (örneğin 3 boğumlu parmak gibi) doğrudan "altın oran" olarak adlandırılmasının matematiksel olarak "zorlama" olabileceği unutulmamalıdır. Diğer bir örnek olarak sarmallarıda verebiliriz. Her sarmal logaritmik değildir ve her logaritmik sarmal altın sarmal değildir. Doğada salyangoz kabuğu veya galaksiler gibi bir çok sarmal yapı gözlemleriz ve bunlar logaritmik özellik gösterirken "altın sarmal" olmaları gerekmez. Her gördüğümüz sarmalı veya her 3-5-8 gibi sayı dizisini hemen "altın oran" etiketiyle damgalamamalıyız. Aslında  "her yerde altın oran var" yanılgısına karşı matematik doğru bir bariyer örmekte.

İkinci nokta doğada phi sayısına ulaşırken benzer yoğunlukta 1/phi 1/phi³ , 3 ve 0.5 gibi diğer değerlerede sık ulaşılmasıdır. Bu husus kritiktir; zira bu yüksek değişkenlik, istatistiksel analizde hata riskini artırır. Çünkü bir çalışmada veriler çok dağınıksa istatistiksel testlerin "arada fark yok" diyerek altın oranı varmış gibi gösterebileceği bilinmelidir. Bu, "sayıları uydurma" riskine karşı teknik bir eleştiridir.

Son olarak (üçüncü nokta), bilimsel çalışmalar sadece phi varlığını gözlemlemekle kalmayıp, olası nedenleri ortata koymalıdır. Örneğin estetikte, altın dikdörtgenin diğer dikdörtgenlerden daha hoş olup olmadığını araştırmakla birliktye çalışma bu fenomenin neden var olduğunu anlamaya çalışmalıdır(. phi’nin görme alanındaki rolü üzerine hipotez). Bu altın oran tartışmasını "mistik bir hayranlıktan" çıkarıp evrimsel bir zorunluluk ve mühendislik optimizasyonu seviyesine taşımaktadır. 

Doğa, "estetik olsun" diye değil, "en az enerjiyle en yüksek performansı versin" diye altın oranı seçmiştir. Altın oran öz-benzerlik, biyolojik büyümeyi ve yönetimi en kolaylaştıran koddur.